What Does Equivalence Mean in Photography?
Back in the film days, nearly every photographer learned on 35mm film cameras, and this was the standard that most enthusiast and even a lot of pros used. Consequently, just about every photographer was familiar with how the 35mm film format would turn out in their final images. Digital has changed this, and we are now seeing a multitude of sensor sizes and formats on the market. This has created a lot of misunderstanding on how to get an equivalent image between different systems. For example, is it possible to obtain the same field-of-view, depth-of-field, and overall noise between Micro Four Thirds, APS-C, and full-frame cameras? Many photographers would assume the answer is no, when in fact it is possible (within certain limitations, described later). In Photography, this is known as equivalence.
In the above example, an equivalent focal length will give you an equivalent field-of-view. In like manner, the equivalent f-stop and ISO will give you the equivalent depth-of-field and noise, respectively. I will address these issues as well as some of the common myths in this article.
Signal-to-Noise Ratio and ISO
The total amount of light reaching the sensor during an exposure is one of the most important factors in how noisy an image will be. This is because of what is referred to as the signal-to-noise ratio. In other words, the greater the amount of light the sensor receives, the greater its signal-to-noise ratio. This means a greater signal and less noise, resulting in a cleaner image.
Let’s examine why this is the case. There are many different sensor types and technologies, including CMOS and CCD imaging sensors, but they all share a few common attributes. Figure 1 shows a very simplified diagram of a typical photosite (loosely referred to as a pixel, since each photosite relates to one pixel in the final image).
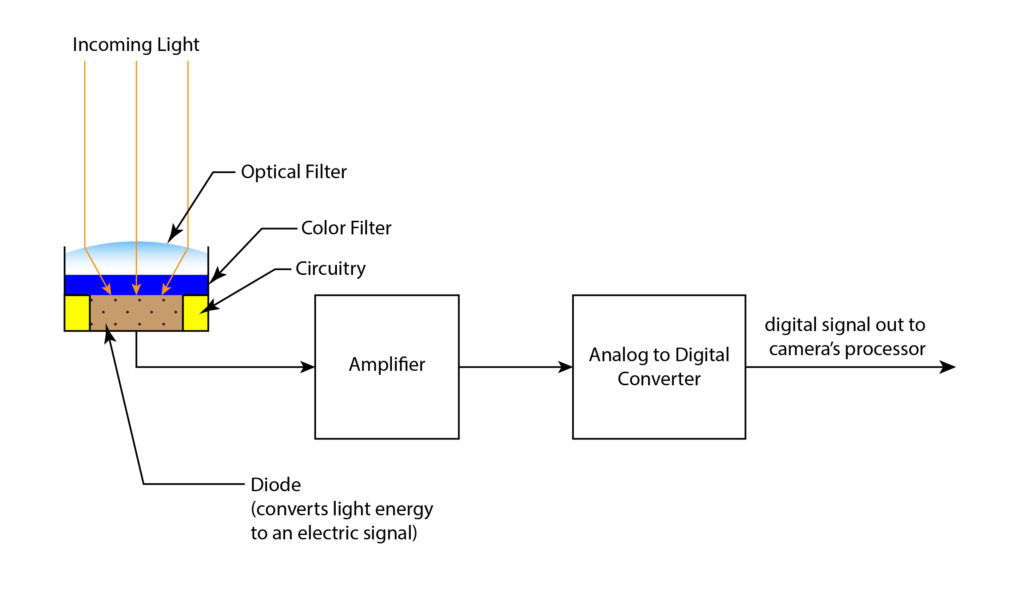
Figure 1
Incoming light is captured by the photosite, which converts the light into a simple electrical current. At this stage, the electrical current is just an analog signal. This electric signal is very weak, so it is amplified before being converted to a digital signal. The amplification is where most of the noise in a digital image is introduced (some noise is also introduced in the analog-to-digital conversion, but that is beyond the scope of this article). This is because, in practice, an analog signal will never be perfectly amplified. Therefore, the signal will be somewhat distorted. And of course, the greater the amplification, the greater the distortion.
This is where adjusting the ISO comes in. Select a higher ISO and you are instructing your camera to increase the amplification. This is the reason why an image appears brighter when a higher ISO is selected, and also why it is noisier. This response is linear, which means that if you double the ISO, from say 100 to 200, the image will appear twice as bright. Or, to maintain the same exposure, let half the light in by using half the shutter speed, or close the aperture by one stop. In conclusion, when you increase the ISO, you decrease the amount of light reaching the sensor.
Keep in mind that the more light that reaches the sensor, the better the image quality because less amplification is needed. If you remember nothing else, remember that increasing the ISO decreases the amount of light reaching the sensor (that, of course, assumes the exposure remains the same by adjusting other image parameters). This decreases the signal-to-noise ratio. Since the light is what produces the signal, you will end up with less signal and more noise.
It is very important to understand that ISO is a measure of how much light is collected per unit area, not the total amount of light collected. To illustrate this, I like to use the bucket in the rain metaphor. Figure 2 shows two buckets of varying sizes collecting rain.
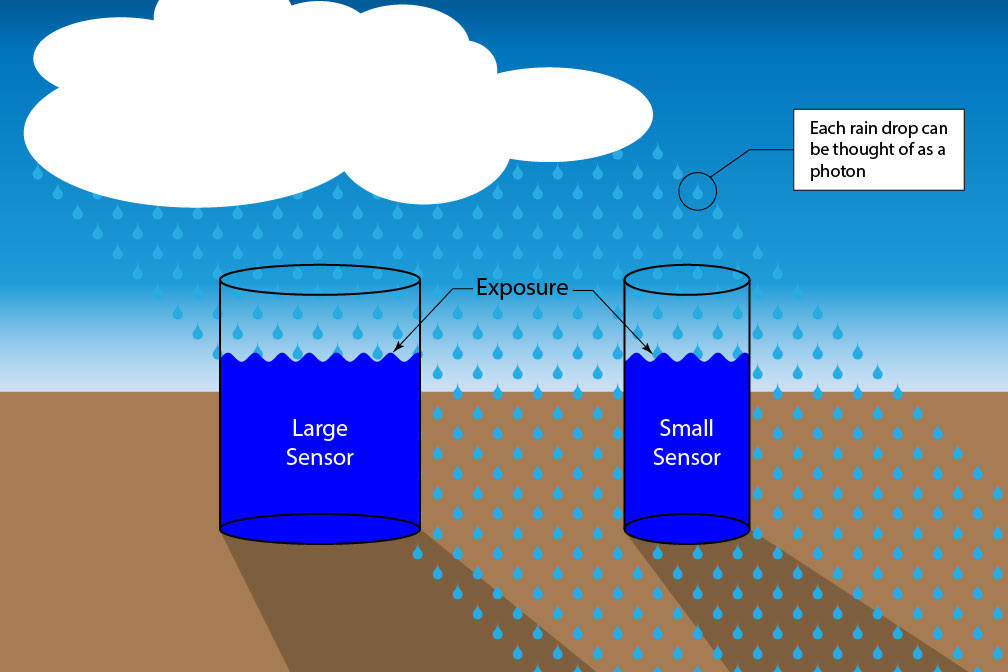
Figure 2
The water level is the same for both buckets shown in Figure 2, but the larger bucket clearly collects a greater volume. Now imagine the buckets as digital sensors, and the drops of rain as photons. In that case, the volume of water in each bucket represents the amount of light collected, and the level of water represents the exposure. To obtain a higher water level, you would have to leave the buckets out in the rain longer. We can see how a smaller sensor will produce an image with the same exposure as a larger sensor even though the total light collected was less.
Relationship Between ISO and Sensor Size
We can now see how the ISO and the physical size of the sensor are dependent upon each other. It is a common misconception that at the same ISO, cameras with different sensor sizes will collect the same amount of light. However, as has been shown above, that is not true. Let’s look at a real-world example to demonstrate this concept.

Figure 3
Both images in Figure 3 were taken with the same camera settings (ISO, f-stop, and shutter speed), but with different sensor sizes. Both images have the same exposure since ISO is a measure of light collected per unit area. However, the total amount of light collected was not the same for each image. The smaller image was taken with a wider-angle lens, so the same scene was shrunk down to fit on a smaller sensor. Another metaphor would be two identical paintings except for their respective canvas sizes. A greater amount of paint would be required for the larger painting.
To summarize, different sensor sizes will give the same exposure for the same ISO (assuming the shutter and aperture are also set to the same values, of course), but the total amount of light collected will be different. Therefore, the images are NOT said to be equivalent.
Equivalent ISO
By selecting an equivalent ISO, it is possible for the smaller sensor to receive the same amount of light as the larger sensor. The f-stop also needs to be adjusted to provide an identical exposure, a topic which will be discussed later. The equivalent ISO is related to the physical area of the sensors as follows:
![]()
Equation 1
For example, the area of a full-frame sensor is 864mm2, and the area of an APS-C sensor is 329mm2. That means that if we use an ISO of 800 on a full-frame sensor, the equivalent ISO would be (384/864)(800) = 356, which would be rounded to the nearest 1/3 stop of ISO 320 (this is because you cannot select ISO 356 on most cameras, so round to the nearest 1/3 stop).
An easier equation for calculating the equivalent ISO is shown below, and is what I use when making all my equivalent ISO calculations. This equation is especially handy since it makes memorizing the different sensor dimensions unnecessary:
![]()
Equation 2
If the respective sensors are not symmetric, then equation 2 is only approximate, but plenty close enough since you must round to the nearest 1/3 stop anyways. Returning to the example above except this time using Equation 2, we have 800/1.52 = 356, or rounded to the nearest 1/3 stop, ISO 320. Therefore, the signal-to-noise ratio, and consequently the noise in the image, will be identical if we use ISO 320 on an APS-C sensor and ISO 800 on a full-frame sensor. The images are equivalent.
Let’s illustrate this concept by going back to the bucket in the rain metaphor, this time shown in Figure 4, which can be thought of as two sensors collecting light. One is a full-frame sensor set to ISO 800, and the other is an APS-C sensor set to ISO 320. We know that if we lower the ISO, we can leave the shutter open longer and collect more light. This is comparable to leaving the bucket out in the rain longer collecting more rain drops (photons in our metaphor). The larger bucket was not left out in the rain as long, but notice that it collected the same total amount of rain due to its larger size.
Although the water level in the larger bucket in Figure 4 is lower, the amplification is greater. Therefore, the water it received is amplified to give it the same water level as the smaller bucket. In turn this gives the final images the same overall exposure.
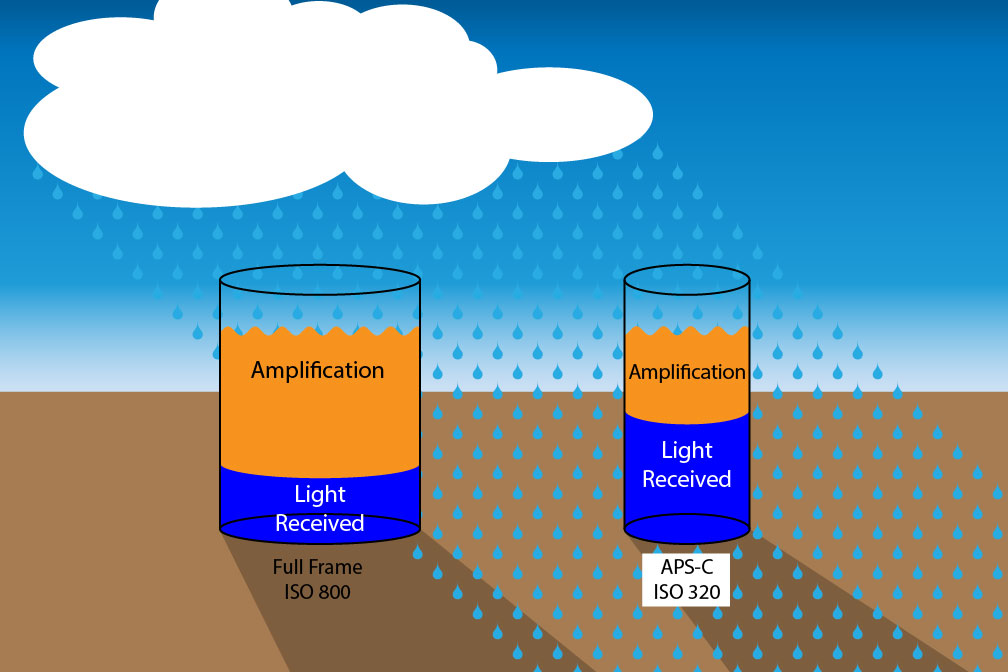
Figure 4
Are Smaller Sensors Noisier?
At this point, I want to take a short detour and address a very common (and understandable) myth about smaller sensor cameras. According to the myth, smaller sensors are noisier than larger sensors. At this point, we know that if both sensors collect the same amount of light, they will have the same signal-to-noise ratio. Let’s look at a couple of images to demonstrate this point. In Figure 5, both images were shot at ISO 800. Notice that the APS-C image is noisier than the full-frame image. Now have a look at Figure 6, where the APS-C image was shot at ISO 320 and the full-frame image was shot at ISO 800. Notice that both images look approximately the same. That is because they were taken at the equivalent ISO with respect to each other, which allowed each image to receive the same total amount of light. Both images in Figures 5 and 6 have been scaled to represent the same percentage of the sensor.
On a side note, the noise per photosite is not affected by the physical size of the sensor. This can be demonstrated using the measurements from DxOMark for the full-frame 51-mega pixel Canon 5DS R and the 20-mega pixel APS-C Canon 7D Mark II. I chose these cameras because they have approximately the same pixel pitch (4.13μm and 4.08μm, respectively), correlating to a pixel size of 17.06μm2 and 16.65μm2. When looking at the noise per pixel at ISO 6400, they perform almost identically, with a signal-to-noise ratio of 20.0 dB and 20.2 dB, respectively. This is despite the 7D Mark II having a smaller sensor. I will discuss noise and pixel density later.
Click on images blow for full-sized JPEG.
Figure 5
Figure 6
In conclusion, the size of the sensor has nothing to do with the overall image quality. What does matter is the amount of light the sensor receives, irrespective of its size. Therefore, a smaller sensor is noisier only when shot at the same ISO as a larger sensor. When an equivalent ISO is used, the two sensors will produce the same level of noise.
Equivalent F-stop
We have seen that we can decrease the ISO for a smaller sensor and obtain the same noise. Back to the bucket in the rain metaphor, this means that the bucket is being left out in the rain longer. In practical terms, this means we are using a longer shutter speed. However, what if we want to use the same shutter speed and still get the same exposure? In the bucket in the rain metaphor, that means it would have to rain harder for the smaller bucket than it would for the larger bucket. In the real world, this means we would open the aperture, or f-stop, allowing a greater amount of light to pass through the lens and reach the sensor. This is what is referred to as the equivalent f-stop. I have written an entire article about the f-stop if you want to learn more about it.
Two important parameters will be impacted by adjusting the f-stop: the amount of light that reaches the sensor, and the depth-of-field. Both will be explored in this section. I have written an entire article describing depth-of-field in much greater detail than what I will discuss here.
Therefore, we must have an equivalent f-stop providing equivalent image parameters for:
- ISO and exposure
- Depth-of-field
By happy coincidence, it turns out that the same equivalent f-stop works for both the ISO and the depth-of-field.
I need to make another important point before going any further. The f-stop, just like the ISO, is a measure of how much light reaches the sensor per unit area, not the total amount of light. Referring back to Figure 2, both the full-frame and APS-C cameras, when set to the same shutter speed, f-stop, and ISO, will give their respective sensors the same amount of light per unit area. However, the total amount of light will be greater for the full-frame camera. Now it is time to explain how to calculate the equivalent f-stop.
It turns out that the math for calculating the equivalent f-stop is very simple.
![]()
Equation 3
For example, the crop factor for an APS-C is 1.5. To calculate the equivalent of f/5.6 on a full-frame:
![]()
(Note that, once again, I am rounding to the nearest 1/3 f-stop, as 5.6/1.5 = 3.73). Therefore, f/3.2 on an APS-C is the equivalent to f/5.6 on a full-frame. If you do the math, you can see that f/3.2 will allow 2.25 times more light to pass through the lens than f/5.6. Incidentally, a full-frame sensor is 2.25 times the size of an APS-C sensor. Therefore, ISO 320 at f/3.2 gives the same exposure and quantity of light as ISO 800 at f/5.6 (remember that ISO 320 on an APS-C was the equivalent to ISO 800 on a full-frame in our previous examples).
Examples of the equivalent depth-of-field are shown in Figures 7 and 8. You can click on the images for the full-sized JPEG.
Figure 7
Both images in Figure 7 were shot at f/5.6. Notice the difference in background blur between the two images. For reference, both images were shot at ISO 800. Now compare that to Figure 8, where the only difference is that the APS-C image was shot at f/3.2 and ISO 320.
Figure 8
Notice how the background blur looks approximately the same in both images. These two images are equivalent to each other.
This addresses another myth about crop-sensor cameras. One of the advantages people often site with using smaller sensor cameras is that they have greater depth-of-field, which is usually desirable for landscape photography. This is not true, however. You can achieve the same depth-of-field by simply adjusting the f-stop. Of course, this goes both ways, as portrait photographers will cite the advantages of the background blur possible with full-frame cameras. Again, by using an adjusted f-stop, you can achieve the same background blur.
Equivalent Focal Length
Equivalent focal length is another factor when comparing cameras with different sensor sizes. The same focal length will not provide the same field-of-view when used on cameras with different sensor sizes. The math used to calculate the equivalent focal length is very simple:
![]()
For example, to calculate the focal length needed with an APS-C camera to provide the same field of view a 50mm lens would provide on a full-frame camera:
![]()
Therefore, a 50mm lens will give the same field-of-view on a full-frame camera as a 33.3mm lens will on an APS-C camera. Note that 33.3mm can be rounded to 35mm with very similar results, which is usually easier to set on most zoom lenses. Figures 9 and 10 illustrate this point.
Figure 9
Both images in Figure 9 were shot at 50mm. Notice how much more zoomed in the APS-C image appears compared to the full-frame image.
Figure 10
Notice that, in Figure 10, both images have approximately the same field-of-view.
Interestingly enough, using the same focal length and f-stop will not give you the same image when used on different sensor sizes, even when the image from the larger sensor has been cropped to the same dimensions as the smaller sensor. The images in Figure 11 were both shot at 100mm and f/2.8. The full-frame image was cropped to show the same field of view as the APS-C image. If you look closely, you will notice that the image compression is greater in the image shot with a APS-C camera. On a side note, notice how the depth-of-field is the same for both images.
Figure 11
Equivalent Shutter Speed
There will be no need to adjust the shutter speed when an equivalent focal length is used (as described in the previous section). This is because the cameras will be showing the same field-of-view. Therefore, the shutter speed will behave in the same manner.
This is one less thing to worry about when it comes to equivalence.
Some Practical Considerations
While I have discussed some of the myths surrounding crop-sensor cameras, I also need to point out a few of the practical limitations when it comes to equivalence. We have discovered that it is possible to obtain an equivalent image in every respect by adjusting the ISO, f-stop, and focal length between cameras with different sensor sizes. And while this is correct in theory, it is not always possible in practice. This is not due to any physical limitation, but is instead imposed by the camera manufacturers.
Let’s look at some examples. One of the favorite portrait lenses is the 70-200mm f/2.8. An equivalent lens for the Micro Four Thirds format would be a 35-100mm f/1.4, which at the time of this writing does not exist. The closest lenses on the market are the Olympus 40-150mm f/2.8 (80-300mm f/5.6 equivalent to a full-frame), and the Panasonic 35-100mm f/2.8 (70-200mm f/5.6 equivalent to a full-frame). This means that an equivalent background blur is only possible at or above f/5.6, which is generally less than desired for portraits. Another favorite lens amongst portrait photographers is the 85mm f/1.2. An equivalent of f/1.2 for the Micro Four Thirds format would be f/0.6, which would be grossly impractical and, needless to say, does not exist.
Setting the equivalent ISO can be another challenge with crop-sensor cameras. Unfortunately, Micro Four Thirds and APS-C cameras typically have a higher base ISO than full-frame cameras. For example, the full-frame Nikon D810 has a base ISO of 64. The equivalent ISO for Micro Four Thirds and APS-C formats would be 16 and 28, respectively. That is significantly lower than the Micro Four Thirds format Olympus OM-D E-M1 Mark II’s base ISO of 200, which would be the equivalent of ISO 800 on the Nikon D810. Therefore, obtaining an equivalent image from the Olympus OM-D E-M1 Mark II versus the Nikon D810 is possible only when the Nikon’s ISO is at or above 800. Some APS-C cameras such as the Canon 7D Mark II and Nikon D500 fare somewhat better with a base ISO of 100, which is equivalent to ISO 250 on a full-frame camera. The Micro Four Thirds format Panasonic GH4 has a base ISO of 100, which is equivalent to ISO 400 on a full-frame camera. At the time of this writing, however, none of the APS-C or Micro Four Thirds format cameras on the market have a base ISO lower than 100, which is too bad since there is really no reason for the ISO to be limited like this.
In conclusion, there are some practical limitations that will prevent obtaining an equivalent image in some cases (not all cases, however). For some types of photography, such as astrophotography and portraits, a full-frame sensor is still desirable to a crop sensor. In the future, this limitation may be removed when camera manufacturers provide lower base ISO’s and faster lenses. This limitation may not apply to you depending on your style of photography, but be aware that some photographers will still benefit from a larger sensor.
A Couple of Further Questions
1. What about pixel density?
Up to this point, I have said very little about pixel density because it makes little difference in terms of total noise in the final image. I know this concept may be a bit controversial, but remember that the total amount of light captured by the entire sensor is what determines the signal-to-noise ratio for the entire image, and this is not affected by the physical size of the photosites. In higher resolution sensors, the pixel density will be correspondingly higher, which means the individual photosites will be smaller. This means the amount of light available per photosite will be smaller, and the signal-to-noise ratio will be correspondingly higher. However, when the entire image is taken into consideration, the total amount of light collected will be the same regardless of pixel density. In effect, the lower signal-to-noise ratio of the smaller photosites will be averaged out and the total noise in the image will be the same.
We can see this by looking at a pixel grid. Figure 12 shows images taken with a 24-mega pixel Nikon D750, and a 36-mega pixel Nikon D810, both being full-frame cameras. Both images were shot at ISO 6400. The images have been cropped so that each image has the same pixel dimensions. Notice how the image from the higher resolution D810 does look noisier. Of course, you must also understand it is showing a smaller percentage of the total sensor area, in other words the both images are showing the same pixel dimensions.
Figure 12
Figure 13 shows the same images, except that they have now been cropped to show the same percentage of the total sensor. Notice how similar the noise is in the two images regardless of the differences in their pixel density.
Figure 13
The results from this test agree with those from DxOMark. When they measured the signal to noise ratio for each individual pixel at ISO 6400, the D750 had a signal to noise ratio of 23.1 dB versus 21.1 dB for the D810. Therefore, the individual pixels in the D810 are about two thirds of a stop noisier than the pixels in the D750. This makes sense because the photosites for the D750 are significantly larger than the photosites for the D810. However, when signal to noise ratio measurements are taken for the entire sensor, the D750 has a signal-to-noise ratio of 27.9 dB versus 27.7 dB for the D810. So, when the entire sensor has been considered, the noise in the image will be nearly identical regardless of the pixel density.
To conclude, smaller pixels are noisier than larger pixels, but smaller pixels do not mean a noisier image! Again, what matters is the total amount of light that all the pixels receive. I know that can seem counter-intuitive, and that is understandable considering that smaller pixels are typically associated with smaller sensors, and that noise levels are often compared between different cameras with the same ISO settings. However, as we have discovered, the ISO is meaningless without taking the sensor size into consideration. Therefore, we must compare different sensor sizes using the adjusted ISO settings or else we are not getting a fair comparison. Of course, one may bring up the argument that the equivalent ISO will result in a slower shutter speed than what would be obtained on a full-frame camera, and this may be a disadvantage. Again, remember the adjusted f-stop? Keep in mind that if we use both the adjusted ISO and the adjusted f-stop, the shutter speed will remain unchanged. If that is not enough, the depth-of-field will also be identical.
2. What about sensor technology?
I did not say anything about sensor technology either. As a rule, sensor technology improves over time, but improvements tend to be marginal from one year to the next. Over a span of 10 years, however, this can become significant. Figure 14 shows the same image taken with both a 14-year-old 6.3-mega pixel Canon 10D, and a much newer 16 mega-pixel Fuji XT-1. Both images were shot at ISO 1600, which was the highest native ISO the old Canon 10D was capable of. Both images were cropped to show the same percentage of the total sensor area. Notice how noisy the old sensor is compared to the much newer one.
Figure 14
Of course, I used cameras from the same generation for all other examples in this article.
Conclusion
The ISO, f-stop, and focal length can be adjusted between cameras with different sensor sizes, allowing you to obtain what is referred to as an equivalent image: in other words, both images have the same noise, depth-of-field, and field-of-view.
Remember that the ISO and f-stop tell us nothing without knowing the sensor size. The reason why the ISO and f-stop are dependent upon the sensor size is because they tell us the amount of light per unit area, not the total amount of light, that reaches the senor. Keep in mind that the focal length and f-stop are physical parameters of the lens which are determined mathematically, and are independent of the sensor size. In other words, a 50mm f/2.8 lens mounted on full-frame camera is still a 50mm f/2.8 lens when mounted on a crop-sensor camera. The difference is the effect it has on the image. This is because a smaller sensor has less total area, meaning it will collect less total light for the same f-stop and ISO (and have a narrower field-of-view). Therefore, the two images will have the same exposure. The image taken with the crop-sensor camera will not be darker than the image taken with a full-frame camera, even though it collected less light.
Also remember that the noise in an image is directly related to the signal-to-noise ratio, so the less light collected by the sensor, the noisier the image. By lowering the ISO and opening the f-stop, we can allow a smaller sensor to collect the same amount of light as a larger sensor. If these parameters are adjusted correctly, they will give us images that are equivalent to each other in terms of both noise and depth-of-field.
Keep in mind a key point in this article: When comparing lenses mated to different sensor sizes, you must adjust both the equivalent focal length and f-stop. Unfortunately, this is a very common misconception amongst photographers. All too often photographers will compare the equivalent focal length and fail to realize that the f-stop needs to be adjusted as well. For example, one of my favorite lenses for the APS-C format is the Fuji 50-140mm f/2.8 lens. Most photographers would incorrectly assume this lens is comparable to a full-frame 70-200mm f/2.8. An even greater comparison is the full-frame 24-70mm f/2.8 verses a Micro Four Thirds 12-35mm f/2.8. Many people will tout the massive size and weight advantage of the smaller lens, believing they are getting a comparable lens in a much smaller package that fits in their pocket. However, physics does not allow this. A Micro Four Thirds lens that has the light gathering power of a full-frame lens will essentially be the same size and weight as its full-frame counterpart. There is just no way around it. I find it very unfortunate that camera manufacturers do not disclose this fact, because in a respect they are misleading their buyers.

Figure 15
For convenience, I have restated the three necessary equations for equivalence:
Equivalent ISO:
![]()
Equivalent f-stop:
![]()
Equivalent focal length:
![]()












